Water Sort in Haskell

Water Sort is a puzzle game where you have to sort coloured water into bottles. If you haven’t tried it yet, there are many clones of it online or on your phone. I started playing the game a while ago and, after getting a little addicted to it, I decided to implement it in Haskell for fun (and to immunise myself against it).

In this post I’ll give an overview of how I implemented the game with a simple terminal-based UI and a list-based solver which takes advantage of laziness. My goal is to show people that are perhaps not very familiar with Haskell that implementing a simple game like this can be fun and rewarding, and to share a couple cool tricks I learned along the way.

All the code for the game is on GitHub, and I will be linking to various files there throughout the post.

Water Sort

The game starts with a bunch of bottles with colour layers stacked on top of one other along with some empty bottles. The version of the game I played has bottles with four layers of colours and two empty bottles:

The goal of the game is to sort the colours into single bottles:

You progress in the game by pouring the top colour layer of a bottle into another bottle:

However, pouring has some simple restrictions:

1. You can only pour a colour into an empty bottle or a bottle with the same colour on top
2. You cannot overfill bottles

Implementing the game

To implement the game I used a simple variation of the model-view-update pattern, also known as the Elm architecture. In brief, the model is the data structure containing the state of the game, the view is a function which takes the model and renders it to the screen, and the update is a function which takes user inputs and adjusts the model accordingly. The game itself consists of a game loop that repeats either until the bottles are sorted (the player wins) or there are no more available actions (the player loses).

The Model

My first step was to model the game state with data types. The whole game state is captured by the Bottles type, which is a Map of bottles to their identifiers:

type Bottles = M.Map BottleId Bottle

A Bottle is modelled as a list of Colors, where the head of the list corresponds to the topmost colour in the bottle. A BottleId is just a type alias for an Int:

type BottleId = Int
type Bottle = [Color]

Since the game will only support levels of a fixed size, our model only needs to represent about a dozen colours, so I decided to model Color with a sum type:

data Color
  = Yellow
  | White
  | Red
  | LightBlue
  | LightGreen
  | Pink
  | Brown
  | DarkGreen
  | Orange
  | DarkBlue
  | DarkRed

The full code for the model can be found in the Model.hs module.

The View

For simplicity, I chose to use the terminal as the UI for my implementation.

To print colours to the terminal, I used two space characters (which on my terminal roughly form a square) and coloured them using xterm-256 colour codes . The final outcome looks like this:

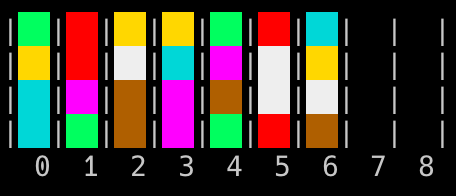
This worked well, but requires one to have a terminal that supports 256 colours and a mono-space font so that two spaces roughly form a square. In code, the function to print a colour looks like this:

showColor :: Color -> String
showColor color = "\x1b[48;5;" <> show (colorCode color) <> "m  \x1b[0m"
  where
    colorCode :: Color -> Int
    colorCode Yellow = 220
    colorCode LightBlue = 44
    colorCode DarkBlue = 21
    colorCode Brown = 130
    colorCode LightGreen = 47
    colorCode DarkGreen = 22
    colorCode Pink = 201
    colorCode White = 255
    colorCode Red = 196
    colorCode Orange = 208
    colorCode DarkRed = 88

colorCode here is a mapping from Color to xterm-256 colour codes. The weird-looking strings on either side of the colour code are the escape codes to set the background colour.

After figuring out how to print a colour, the next challenge was to print the bottles side by side. This is made a little tricky by the fact that the terminal can only print one line at time from top to bottom. My solution was to first transform our Bottles map into a list of Lines and then print them out in order. I modelled a Line as a list of Squares, where each square is either empty, a separator or a colour:

data Square = Empty | Separator | Full Color
type Line = [Square]

Then, I used an unfoldr to generate the list of Lines:

bottlesToGrid :: Bottles -> [Line]
bottlesToGrid = reverse . unfoldr makeLine . map reverse . M.elems
  where
    getSquare :: Bottle -> Square
    getSquare = maybe Empty Full . headMaybe

    makeLine :: [Bottle] -> Maybe (Line, [Bottle])
    makeLine xs
      | all null xs = Nothing
      | otherwise = Just (map getSquare xs, map tailSafe xs)

This function works by constructing the rows from the bottom of the bottles to the top, and then reversing the order of the rows at the end. The unfoldr uses a makeLine function which takes a list of Bottles and constructs a single line from it. The line is constructed by mapping over the bottles with the getSquare function, which returns an Empty square if the bottle is empty and a Full square with the colour if it’s not. If all the bottles are empty, makeLine returns Nothing to signal the end of the unfold. I also used two helper functions:

• headMaybe :: [a] -> Maybe a is a safe version of head that returns Nothing when given an empty list
• tailSafe :: [a] -> [a] is a version of tail that returns an empty list when given an empty list.

The final step was to actually make the functions to convert the lines to strings which can then be printed to the terminal:

showSquare :: Square -> String
showSquare Empty = "  "
showSquare Separator = "|"
showSquare (Full color) = showColor color

showLine :: Line -> String
showLine line =
  let sepLine = [Separator] <> intersperse Separator line <> [Separator]
   in concatMap showSquare sepLine

Check out View.hs file for the full code to show the game.

The Update

Players in this game can only make a single type of action: a pour from one bottle to another. Pours are modelled with a product type of two bottle ids:

data Pour = Pour
  { from :: BottleId
  , to :: BottleId
  }

Each turn, the user is asked to input a pour as two numbers separated by an arrow (for example "2 -> 3"). The game then takes the line as input, splits it on the "->" string and parses the two numbers on either side:

parsePour :: String -> Either GameError Pour
parsePour line = case splitOn "->" line of
  [from, to] -> do
    fromBottle <- maybeThrow (InvalidBottleId from) (readMaybe from)
    toBottle <- maybeThrow (InvalidBottleId to) (readMaybe to)
    pure (Pour fromBottle toBottle)
  _ -> Left (InvalidInput line)

Parsing errors are handled explicitly by returning an Either GameError Pour. GameError here is a sum type that captures all the logical errors that can occur in the game:

data GameError
  = InvalidPuzzleType String
  | InvalidBottleId String
  | InvalidInput String
  ...

In larger projects it could be a good idea to split up error types into several smaller types, but for a small project like this I decided that having a single error type was good enough.

I also chose to use Either as a simple mechanism to throw and handle errors in pure functions. “Throwing an error” is implemented by returning a Left, which then short-circuits the rest of the function thanks to the Either monad instance. Errors that crop up are handled in the top-level game loop. I also made two functions for convenience:

maybeThrow :: GameError -> Maybe a -> Either GameError a
maybeThrow err Nothing = Left err
maybeThrow _ (Just a) = Right a

whenThrow :: Bool -> GameError -> Either GameError ()
whenThrow True err = Left err
whenThrow False _ = Right ()

Once a Pour is received and parsed from the user it is passed to the update function which contains the main model update logic:

update :: Bottles -> Pour -> Either GameError Bottles
update bottles pour@(Pour from to) = do
  (fromBottle, toBottle) <- getPourBottles bottles pour
  (fromHead, fromTail) <- validate pour fromBottle toBottle
  let insertFrom = M.insert from fromTail
  let insertTo = M.insert to (fromHead <> toBottle)
  pure . insertFrom . insertTo $ bottles

This function essentially get the two bottles from the game state, check that the pour is valid, splits the colours in the from bottle into the part that will be poured into the to bottle and the part that will stay, and then updates the game state with the new bottles. getPourBottles and validate help with doing that and contain most of the logic that ensures that the pour follows what is allowed by the rules of the game.

The full code for the update is in the Update.hs module.

Putting it all together

Time to combine the components into the game loop! The body of the loop is contained in the step function:

step :: Bottles -> IO Bottles
step bottles = do
  putStrLn (showGame bottles)
  line <- getLine
  case (parsePour line >>= update bottles) of
    Right newBottles -> pure newBottles
    Left gameError -> do
      print gameError
      pure bottles

In other words, for each iteration:

1. Show the current state of the game
2. Ask the user for input
3. Parse the input
4. Update the game state based on the input

If an error comes up in step 3 or 4, the game shows the error to the user and reverts back to the start of the turn.

The last part is the actual game loop itself, which I implemented as a recursive function which repeatedly calls itself until the game is over:

loop :: Bottles -> IO Bottles
loop bottles = do
  newBottles <- step bottles
  if gameOver newBottles
    then pure newBottles
    else loop newBottles

The code for the game loop is in Main.hs.

Creating puzzles

Now that I had a working game, I needed a way to generate new puzzles so that users (me, myself and I) can play the game to their heart’s content. To help learn the game, I also decided to support three puzzle sizes:

data PuzzleSize = Small | Medium | Large

Given a puzzle size, the next thing to do is to pick which (and how many) colours to use in the puzzle. I arbitrarily decided on 4, 7, and 10 colours for the small, medium, and large puzzles respectively, and used toEnum from the Enum class to make the list of colours of the appropriate size:

colorPalette :: PuzzleSize -> [Color]
colorPalette Small = map toEnum [0 .. 3]
colorPalette Medium = map toEnum [0 .. 6]
colorPalette Large = map toEnum [0 .. 9]

The puzzles start with the same number of full bottles as the number of colours. Mirroring the version of the game I’ve been playing, I decided to use bottles of height 4 and to add 2 extra empty bottles at the start.

I ended up with the following function to make a new random assortment of bottles:

randomBottles :: MonadRandom m => PuzzleSize -> m Bottles
randomBottles size = do
  let initColors = concat (replicate 4 (colorPalette size))
  randomColors <- shuffle initColors
  let bottles = chunksOf 4 randomColors <> [[], []]
  pure (M.fromList $ zip [0 ..] bottles)

In words, randomBottles:

1. Makes a list with 4 copies of each colour
2. Shuffles it
3. Splits it into a list of bottles of height 4
4. Adds two empty bottles
5. Converts the list into a Map

But, you might ask: how do you know that the puzzle is actually solvable? Interestingly, after some Googling I discovered that some mathematicians actually studied this problem and found some bounds for the minimum number of empty bottles needed to ensure the puzzle is always solvable. Plugging in our parameters, two empty bottles seems to be the exact lower bound for all three puzzle sizes. Cool! But that still doesn’t guarantee that the puzzle has a solution.

Instead, I went for a cruder approach and made a function that makes random puzzles and tries to solve them until it finds one that has a solution:

createPuzzle :: MonadRandom m => PuzzleSize -> m Bottles
createPuzzle size = do
  bottles <- randomBottles (sizeToInt size)
  if isJust (solve bottles)
  then pure bottles
  else createPuzzle size

In practice most random puzzles seem to be solvable, and in the worst case where the puzzle is not solvable or the solver is being really slow the user can just restart the game.

Solving the game

To solve the game one needs to find a sequence of pours that will sort an initial set of bottles (where possible). I implemented the solver as follows:

solve :: Bottles -> Maybe [Pour]
solve = fmap (reverse . history) . headMaybe . solutions . SolverState []

The first thing this function does is to transform the input Bottles into a SolverState, which is a record of the current game state and the history of pours that led to it:

data SolverState = SolverState
  { history :: [Pour]
  , current :: Bottles
  }

The function then passes the initial solver state to the solutions function, which is where most of the magic happens:

solutions :: SolverState -> [SolverState]
solutions state
  | gameOver (current state) = pure state
  | otherwise = do
      (pour, newBottles) <- possiblePours (current state)
      solutions (SolverState (pour : history state) newBottles)

The solutions function returns a list of all possible solution states coupled with their pour history. Given a solver state, it first checks if the game is over using the same function as before. If the game is indeed over, it returns the current solver state and stops the recursion. Otherwise, it finds the list of all valid pours from the current state and recursively calls solutions on each of them [1]. In this way, it traverses the entire tree of possible sequences of pours, gathering all the solutions as it goes.

The list of valid pours is created by the possiblePours function, which first creates a list of all possible pours and then filters out the invalid ones using mapMaybe and tryPour:

possiblePours :: Bottles -> [(Pour, Bottles)]
possiblePours bottles =
  let bottleIds = M.keys bottles
      pours = liftA2 Pour bottleIds bottleIds
   in mapMaybe (tryPour bottles) pours

As its name implies, the tryPour function “tries” to perform a pour in the current game state using the update function from before, and returns Nothing if the pour is not successful:

tryPour :: Bottles -> Pour -> Maybe (Pour, Bottles)
tryPour bottles pour =
  case update bottles pour of
    Left _ -> Nothing
    Right newBottles -> Just (pour, newBottles)

Infinite cycles, for example where a colour is poured back and forth between two bottles forever, are prevented by an extra check in the update function that ensures these types of pours are considered invalid. In turn, this ensures that the solutions function is always guaranteed to terminate.

However, traversing the entire tree of possible pour sequences can quickly become computationally infeasible. This is where the second bit of magic comes in: thanks to Haskell’s laziness, taking the head of the list of possible solutions with headMaybe means that we actually only compute the first solution and leave the rest as thunks, effectively morphing the solver into a depth-first search [2]! Neat right?

The final step taken by solve is to extract the pour history from our solution state and to reverse it to get the correct order of pours. The full code for the solver is contained in the Solver.hs module.

Next steps

Although the game is playable at this point there are still lots of things one could improve. Here are some ideas:

• Undo - Add a way to undo a move. At the moment players have no way to backtrack if they make a mistake, which can quickly get annoying
• Save - Add a way to save a puzzle and come back to it later. This could even be used to share puzzles with others
• Web - Make it playable on the web! It should be straightforward to port the game to PureScript and make a simple UI for it
• Tests - Add some tests to ensure that our implementation actually respects the rules of the game

And that’s it! Hope you enjoyed coming on this this little journey with me and maybe even learned a new trick or two along the way.

[1] I used the monad instance for lists here, but I could have just as easily used a list comprehension instead:

solutions :: SolverState -> [SolverState]
solutions state
  | gameOver (current state) = pure state
  | otherwise =
      concat
        [ solutions (SolverState (pour : history state) newBottles)
        | (pour, newBottles) <- possiblePours (current state)
        ]

[2] I used lists and laziness in this case because it was the simplest way I could think of to implement and explain the solver. However, using lists in this way could still consume tons of memory as it keeps track of previous unsuccessful branches in memory (I think). Instead, one could use Maybe and its MonadPlus instance to implement a constant-space search.

If you have feedback or find any mistakes, feel free drop an issue on Github or to email me at nicolas.audinet@chalmers.se !